洛谷P1616题解:动态规划之完全背包问题

一、题目解读
洛谷P1616题要求在一个包含M个活动(每个活动有固定时间和价值)的场景中,求解在总时间T内选择活动的最优组合,使得总价值最大化。活动可重复选择,需利用动态规划算法找到最优解。题目强调时间限制与价值收益的平衡,属于典型的完全背包问题变体。
二、解题思路
1. 动态规划核心思想:将问题拆解为子问题,通过状态转移方程逐步求解全局最优解。
2. 完全背包模型:与01背包不同,完全背包允许每个物品(活动)被选择多次,因此状态转移需考虑重复选择的可能性。
3. 优化策略:使用一维DP数组(空间优化),通过正序遍历容量(时间)实现状态更新,避免重复计算。
三、解题步骤
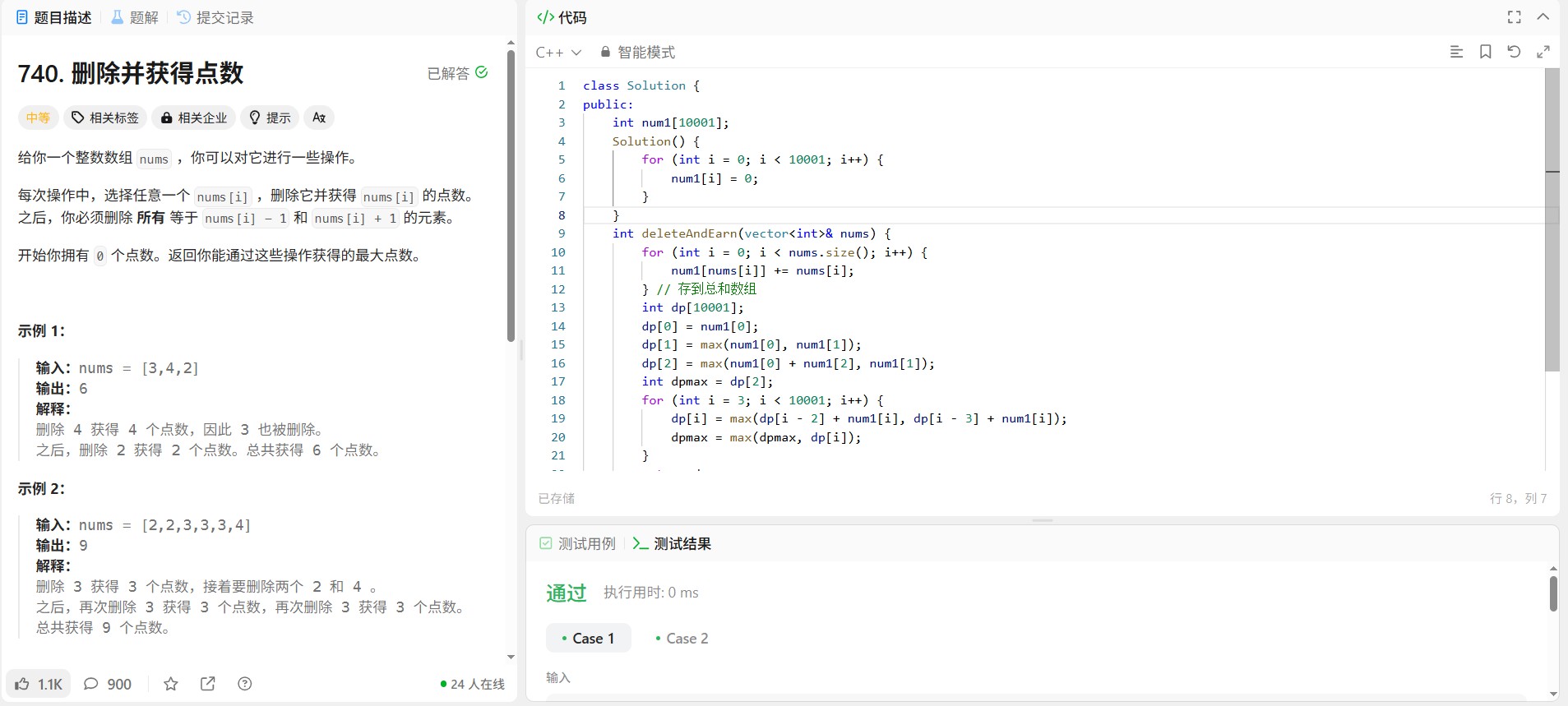
1. 数据输入与初始化:
○ 读取总时间T和活动数量M。
○ 使用vector存储每个活动的时间time和价值value。
○ 初始化DP数组dp,其中dp[j]表示在时间j内可获得的最高价值。
2. 动态规划循环:
○ 外层遍历活动(物品),内层正序遍历时间(容量)。
○ 状态转移方程:dp[j] = max(dp[j], dp[j - time[i]] + value[i]),即当前时间j的价值可选择“不选该活动”或“选该活动并扣除其时间后剩余价值+当前价值”。
3. 输出结果:dp数组的最后一个元素dp[t]即为最优解。
四、代码与注释
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main() {
int t, m; // t为总时间,m为活动数量
cin >> t >> m;
vector<int> time(m), value(m); // time存储活动时间,value存储活动价值
for (int i = 0; i < m; ++i) {
cin >> time[i] >> value[i];
}
vector<long long> dp(t + 1, 0); // dp[i]表示前i时间内的最大价值,初始化为0
// 完全背包核心算法
for (int i = 0; i < m; ++i) { // 遍历每个活动
for (int j = time[i]; j <= t; ++j) { // 正序遍历时间(容量)
dp[j] = max(dp[j], dp[j - time[i]] + value[i]); // 状态转移:选择当前活动或不选择
}
}
cout << dp[t] << endl; // 输出最终结果
return 0;
}五、总结
本文通过动态规划方法解决了洛谷P1616题中的时间价值优化问题,利用完全背包模型允许重复选择的特点,通过简洁的状态转移方程实现了高效求解。代码采用一维DP数组降低空间复杂度,正序遍历确保重复选择的有效性。该解法为同类背包问题提供了通用框架,需重点理解状态定义与转移逻辑,适用于资源可重复利用的最优决策场景。
原创内容 转载请注明出处