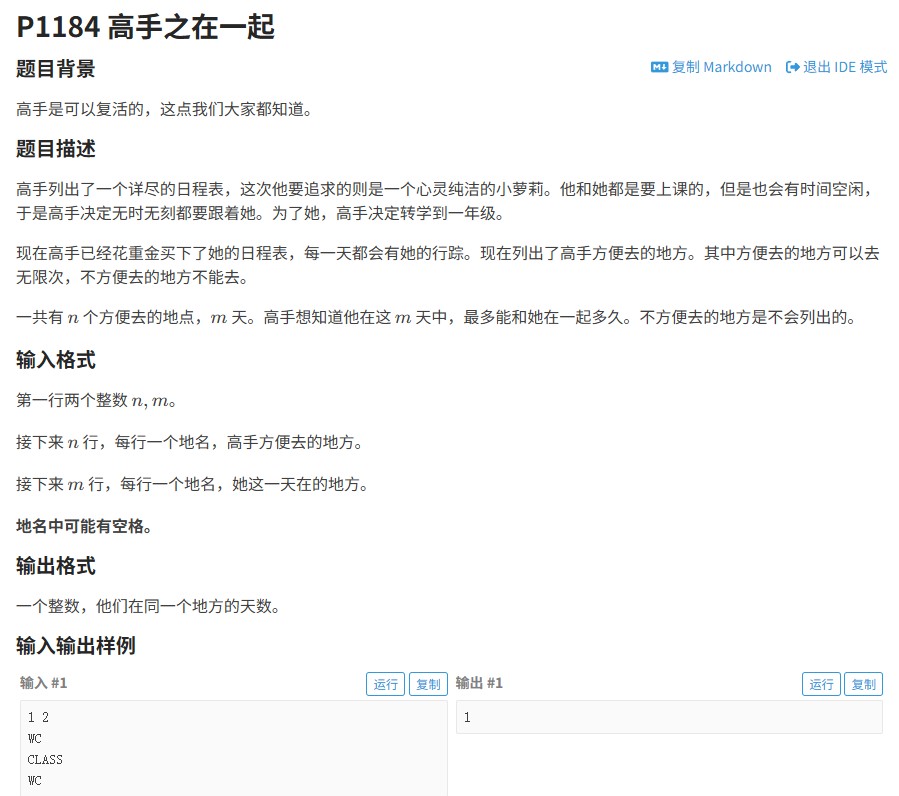
力扣94：递归之美 轻松掌握二叉树中序遍历

题目解读

二叉树的中序遍历是一种基础且重要的树遍历方式，其遍历顺序为：先递归地中序遍历左子树，然后访问根节点，最后递归地中序遍历右子树。对于二叉搜索树，中序遍历的结果恰好是节点值的升序排列。给定一个二叉树的根节点，我们需要按照这个顺序访问所有节点，并将它们的值存储在一个列表中返回。这个问题虽然简单，但却是理解更复杂树算法的基础。

解题思路与过程

用递归方法来轻松实现中序遍历。定义一个成员变量ret来存储遍历结果，以及一个辅助函数inorder来完成实际的递归遍历。当遇到空节点时直接返回，否则先递归处理左子树，然后将当前节点的值加入结果列表，最后递归处理右子树。主函数inorderTraversal初始化遍历过程并返回最终结果。

代码实现与注释

class Solution {
public:
    vector<int> ret; // 存储遍历结果的容器
    
    // 递归中序遍历辅助函数
    void inorder(TreeNode* root)
    {
        if(!root) // 递归终止条件：空节点
        {
            return;
        }
        inorder(root->left);     // 递归遍历左子树
        ret.push_back(root->val); // 访问当前节点（根）
        inorder(root->right);    // 递归遍历右子树
    }
    
    // 主函数：初始化遍历过程并返回结果
    vector<int> inorderTraversal(TreeNode* root) {
        inorder(root); // 开始递归遍历
        return ret;     // 返回遍历结果
    }
};