力扣5：中心扩散法 轻松破解最长回文子串

题目解读：

在一个给定的字符串中，我们需要找到最长的回文子串。回文是指正读反读都相同的字符串，如"aba"、"abba"都是回文。这个问题看似简单，但要在字符串中高效地找到最长的回文子串却需要巧妙的算法设计。题目要求我们不仅要找到这样的子串，还要在时间复杂度上尽可能优化。

解题思路与过程：

1.采用中心扩散法来解决最长回文子串问题。首先处理长度为1和2的特殊情况，然后对于更长的字符串，从第三个字符开始，以每个字符为中心向两边扩散寻找回文。

2.处理边界情况：当字符串长度为1时直接返回该字符；长度为2时，如果两个字符相同则返回整个字符串，否则返回第一个字符。对于更长的字符串，检查前三个字符是否形成回文（如"aaa"或"aba"模式）。

3.核心部分从第三个字符开始遍历字符串，对每个字符执行中心扩散：先向左和向右扩展找到所有与中心字符相同的连续字符（处理偶数长度回文的情况），然后继续向两边扩展比较字符是否相同。每次找到更长的回文时，就更新存储的最长回文子串。

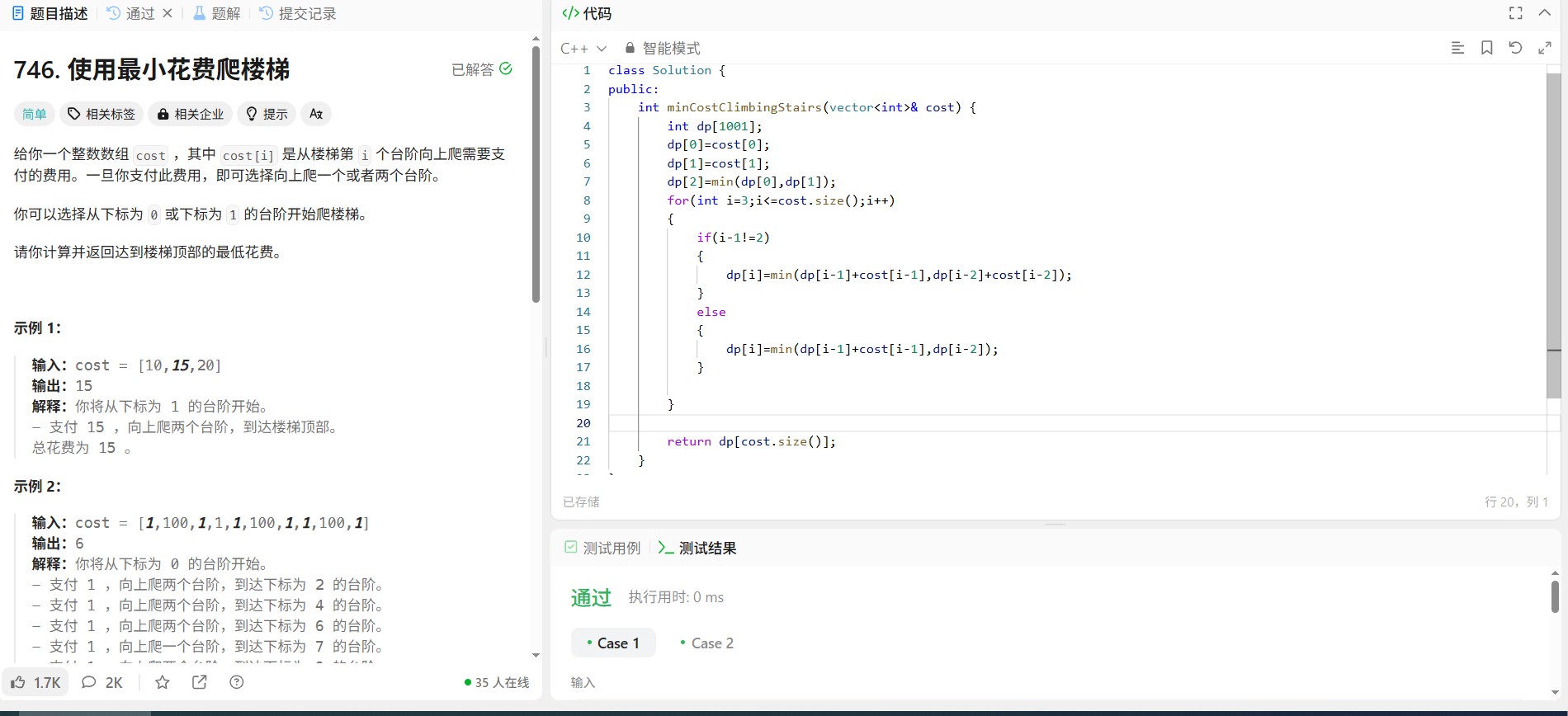
代码：

class Solution {
public:
    string longestPalindrome(string s) {
        string maxs;
        if (s.size() == 1)
            return s; // 回文子串是它本身
        if (s.size() == 2) {
            if (s[0] == s[1])
                return s; // aa
            else {
                string s1 = "";
                s1 = s1 + s[0];
                return s1; // ab
            }
        }
        // x是任意字符，不是字母x
        if (s[0] == s[1]) {            // aax
            maxs = maxs + s[0] + s[1]; // maxs=aa
            if (s[1] == s[2]) {        // aaa
                maxs = maxs + s[2];    // maxs=aaa
            }
        } else {
            if (s[0] == s[2]) {                   // axa
                maxs = maxs + s[0] + s[1] + s[2]; // maxs=axa
            }
        }
        for (int i = 2; i < s.size(); i++) {//以字符i为中心，向两边扩散，获取最长回文串
            int left = 0, right = 0;
            int j = i - 1;
            while (j >= 0 and s[j] == s[i]) { // 向左扩展找到所有相同字符
                j--;
                left--;
            }
            j = i + 1;
            while (j < s.size() and s[j] == s[i]) { // 向右扩展找到所有相同字符
                j++;
                right++;
            }
            //左右指针移动，先判断是否越界再偏移
            j = 1;
            while (i + right + j <= s.size() and i + left - j >= 0 
                   and s[i + left - j] == s[i + right + j]) { // 向两边扩展比较字符
                j++;
            }
            j--;//判断回文
            
            if ((i + right + j) - i - left + j + 1 > maxs.size()) { // 找到更长的回文
                maxs = "";
                for (int k = i + left - j; k <= i + right + j; k++) {
                    maxs = maxs + s[k]; // 构建新的最长回文子串
                }
            }//存储回文
        }

        return maxs;
    }
};