CSP-J方格取数题解|动态规划解法|洛谷P7074代码解析

一、题目解读
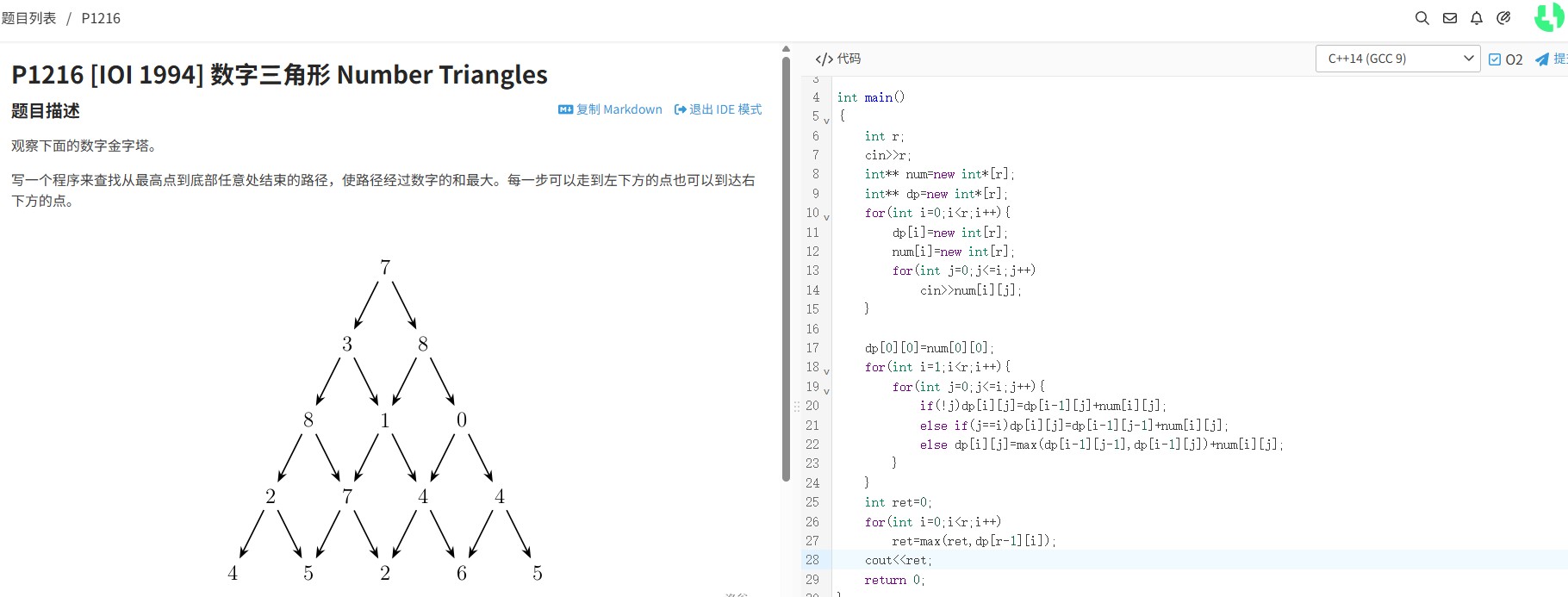
题目要求在一个n×m的网格中,从左上角到右下角选择一条路径,路径上的数字可重复取用,求取数之和的最大值。路径限制为仅能向右或向下移动。需注意路径的灵活性与重复取数的可能性,传统单向动态规划难以直接适用,需设计双向状态转移策略。
二、解题思路
1. 动态规划核心:设计二维状态dp[i][j][k],k=0表示从上方到达(i,j)的最大和,k=1表示从下方到达。
2. 双向处理:先从上到下计算每一列的“从上到达”状态,再从下到上计算“从下到达”状态,利用左右方向的可达性扩展路径。
3. 边界优化:首列仅能从上方转移,末行仅能从下方转移,避免无效计算。
4. 状态转移方程:
从上到达:dp[i][j][0] = max(dp[i][j-1][0], dp[i][j-1][1]) + grid[i][j](左方或下方转移)
从下到达:dp[i][j][1] = max(dp[i][j-1][0], dp[i][j-1][1], dp[i+1][j][1]) + grid[i][j](左方或上方转移)
三、解题步骤
1. 输入与初始化:
读入网格尺寸n×m及数值矩阵grid。
初始化起点:dp[0][0][0] = dp[0][0][1] = grid[0][0],即双向路径均从原点开始。
2. 首列处理:仅能从上方转移,递推公式:dp[i][0][0] = dp[i][0][1] = dp[i-1][0][0] + grid[i][0]。
3. 主体动态规划:
外层循环按列遍历(j=1→m-1)。
内层循环分为两部分:
从上到下计算dp[i][j][0],利用左方或下方状态转移。
从下到上计算dp[i][j][1],利用左方或上方状态转移。
4. 输出结果:最终答案取右下角两种状态的最大值:max(dp[n-1][m-1][0], dp[n-1][m-1][1])。
四、代码与注释
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const int INF = 1e9; // 定义正无穷边界
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr); // 加速IO
int n, m;
cin >> n >> m; // 输入网格尺寸
vector<vector<int>> grid(n, vector<int>(m)); // 存储网格数值
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
cin >> grid[i][j];
}
}
// dp[i][j][0] 表示从上方到达(i,j)的最大和
// dp[i][j][1] 表示从下方到达(i,j)的最大和
vector<vector<vector<long long>>> dp(n, vector<vector<long long>>(m, vector<long long>(2, -INF))); // 初始化状态数组(双向)
// 初始化起点
dp[0][0][0] = dp[0][0][1] = grid[0][0]; // 双向路径均从原点开始
// 处理第一列,只能从上方来
for (int i = 1; i < n; ++i) {
dp[i][0][0] = dp[i][0][1] = dp[i-1][0][0] + grid[i][0]; // 首列仅依赖上方状态
}
// 动态规划处理
for (int j = 1; j < m; ++j) { // 按列遍历
// 从上到下处理当前列
for (int i = 0; i < n; ++i) {
// 可以从左边来
if (i == 0) { // 边界情况:第一行仅依赖左方
dp[i][j][0] = max(dp[i][j-1][0], dp[i][j-1][1]) + grid[i][j];
} else { // 一般情况:综合左方或下方状态
dp[i][j][0] = max({dp[i][j-1][0], dp[i][j-1][1], dp[i-1][j][0]}) + grid[i][j];
}
}
// 从下到上处理当前列
for (int i = n-1; i >= 0; --i) {
// 可以从左边来
if (i == n-1) { // 边界情况:末行仅依赖左方
dp[i][j][1] = max(dp[i][j-1][0], dp[i][j-1][1]) + grid[i][j];
} else { // 一般情况:综合左方或上方状态
dp[i][j][1] = max({dp[i][j-1][0], dp[i][j-1][1], dp[i+1][j][1]}) + grid[i][j];
}
}
}
cout << max(dp[n-1][m-1][0], dp[n-1][m-1][1]) << endl; // 输出终点状态最大值
return 0;
}五、总结
1. 关键点:通过双向动态规划打破传统单向路径限制,利用状态分离实现灵活取数。
2. 优化技巧:
利用边界特性(首列/末行)减少无效计算。
使用max({})语法简化多值比较,提升代码可读性。
3. 扩展思考:若允许斜向移动,需设计更高维状态,或采用图论算法求解。
该解法通过清晰的逻辑与高效的状态设计,为类似路径规划问题提供了优秀范例。
原创内容 转载请注明出处