力扣119题：从O(n²)到O(2n)：杨辉三角高效空间优化

题目重解:

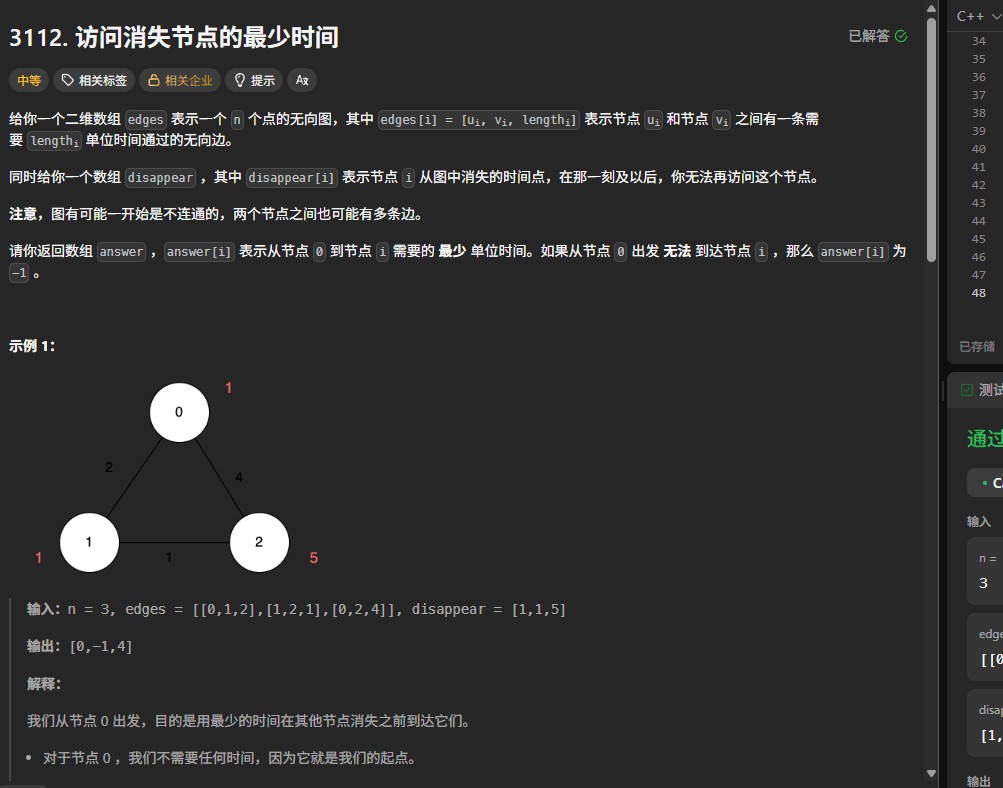
给定一个非负索引 rowIndex，返回杨辉三角的第 rowIndex 行。不同于生成整个杨辉三角，这道题要求我们只返回特定行，且空间复杂度应尽可能优化。例如输入3，需要返回[1,3,3,1]。

解题思路:

1.使用两个一维数组交替存储当前行和上一行数据

2.通过now/pre指针和异或运算实现数组切换

3.首尾元素固定为1，中间元素由上一行相邻元素相加得到

4.最终只需保留最后计算的行数据

代码详解：

class Solution {
public:
    vector<int> getRow(int rowIndex) {
       int a[2][34]; // 双数组存储空间
       int now=1;    // 当前写入数组索引
       int pre=0;    // 上一行数据数组索引
       a[pre][0]=1;  // 初始化第0行
       
       // 逐行计算
       for(int i=1;i<=rowIndex;i++) {
            for(int j=0;j<=i;j++) {
                if(j==i or j==0) {  // 首尾元素为1
                    a[now][j]=1;
                }
                else {  // 中间元素=上一行相邻元素之和
                    a[now][j]=a[pre][j]+a[pre][j-1];
                }
            }
            now^=1;  // 位运算切换数组
            pre^=1;  // 等价于now=(now+1)%2, pre=(pre+1)%2
       }
       
       // 组装结果
       vector<int> v;
       for(int i=0;i<=rowIndex;i++) {
            v.push_back(a[pre][i]); // 注意最后使用pre指针
       }
       return v;
    }
};