牛客NC67题解：汉诺塔递归算法与解题步骤

一、题目解读

牛客NC67题要求解决汉诺塔问题，这是一个经典的递归算法题目。题目给定整数n，代表汉诺塔中的盘子数量，需要输出将n个盘子从起始柱移动到目标柱的所有步骤。汉诺塔问题规则为：每次只能移动一个盘子，且大盘子不能放在小盘子之上。理解题目本质和递归特性是解题关键。

二、解题思路

采用递归方法解决汉诺塔问题。核心思想是将n个盘子的移动分解为三个步骤：

1. 将n-1个盘子从起始柱（from）借助目标柱（to）移动到辅助柱（aux）；

2. 将第n个盘子直接从起始柱移动到目标柱；

3. 将n-1个盘子从辅助柱借助起始柱移动到目标柱。

递归的终止条件为n=1时，直接移动单个盘子。

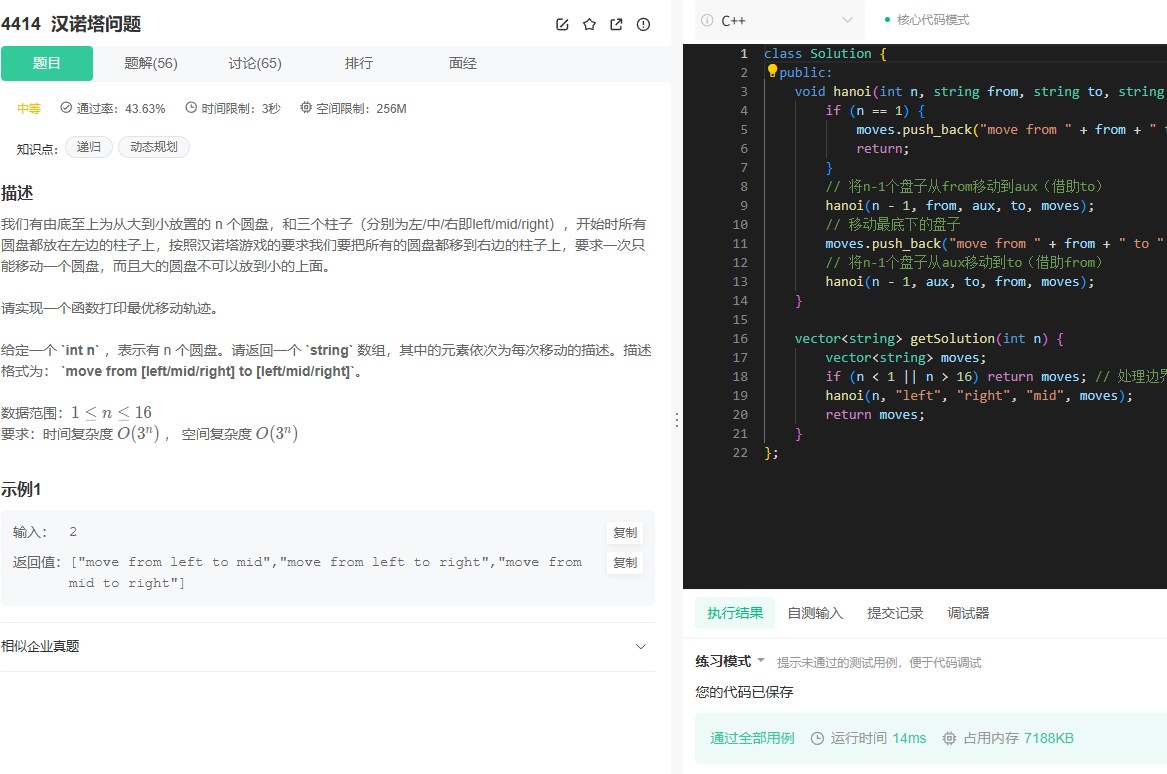
三、解题步骤

1. 初始化：创建空向量moves用于存储移动步骤。

2. 调用递归函数：hanoi(n, "left", "right", "mid", moves)，其中参数分别表示盘子数量、起始柱、目标柱、辅助柱和步骤容器。

3. 递归执行：

    当n=1时，执行基础操作，将步骤"move from X to Y"加入moves并返回。

    当n>1时，递归调用自身三次：先将n-1个盘子移到辅助柱，再移动第n个盘子，最后将n-1个盘子从辅助柱移到目标柱。

4. 返回结果：最终moves包含所有移动步骤，按顺序输出。

四、代码和注释

class Solution {
public:
    vector<string> getSolution(int n) {
        vector<string> moves;
        hanoi(n, "left", "right", "mid", moves); // 初始化递归调用
        return moves;
    }

    void hanoi(int n, string from, string to, string aux, vector<string>& moves) {
        if (n == 1) { // 基础情况：单个盘子直接移动
            moves.push_back("move from " + from + " to " + to);
            return;
        }
        // 递归三步走
        hanoi(n - 1, from, aux, to, moves); // 步骤1：移动n-1个盘子到辅助柱
        moves.push_back("move from " + from + " to " + to); // 步骤2：移动第n个盘子
        hanoi(n - 1, aux, to, from, moves); // 步骤3：移动n-1个盘子到目标柱
    }
};

五、总结

通过递归方法，汉诺塔问题被巧妙分解为子问题，代码简洁且逻辑清晰。关键在于理解递归的“大问题拆解”思路，以及三个步骤的先后顺序。在实际应用中，递归算法需注意栈溢出风险（对于超大n值），但本题中n的范围通常可控。掌握此类递归模型有助于解决类似需要分治策略的问题。