力扣1137题：动态规划解泰波那契数 高效求解第N项的秘密

一：重新解读题目

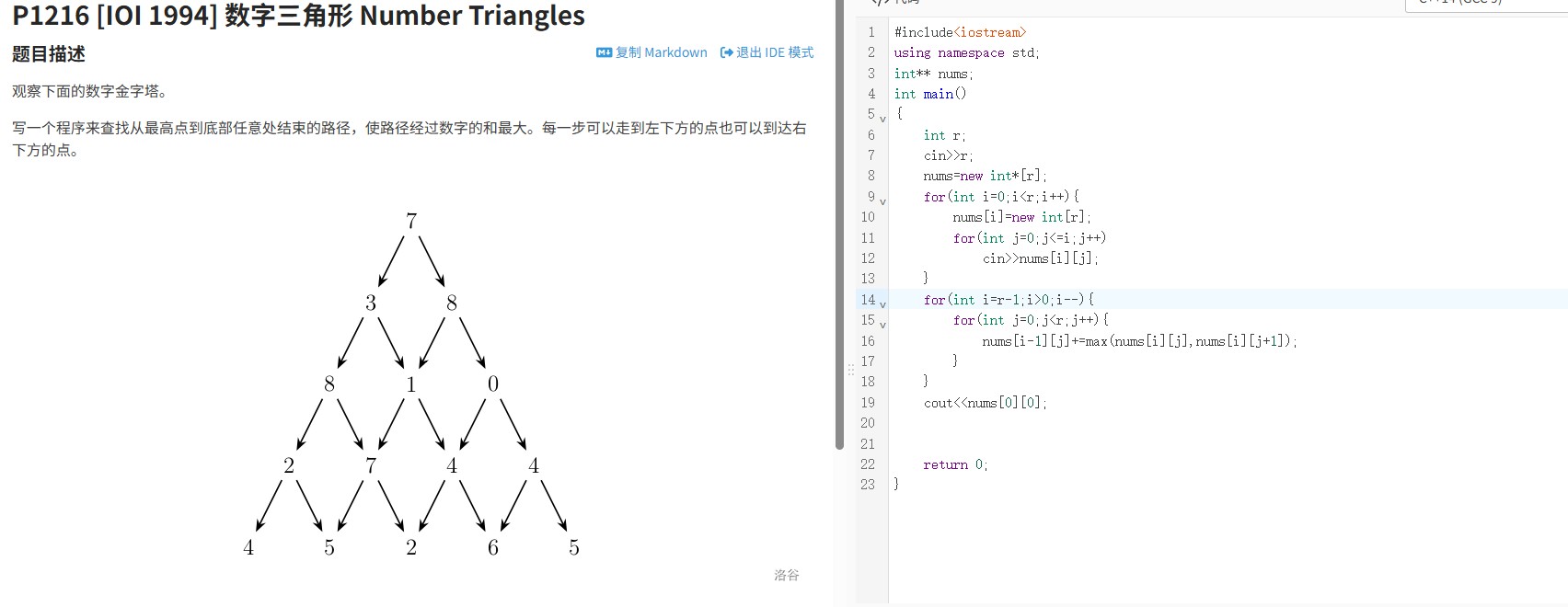
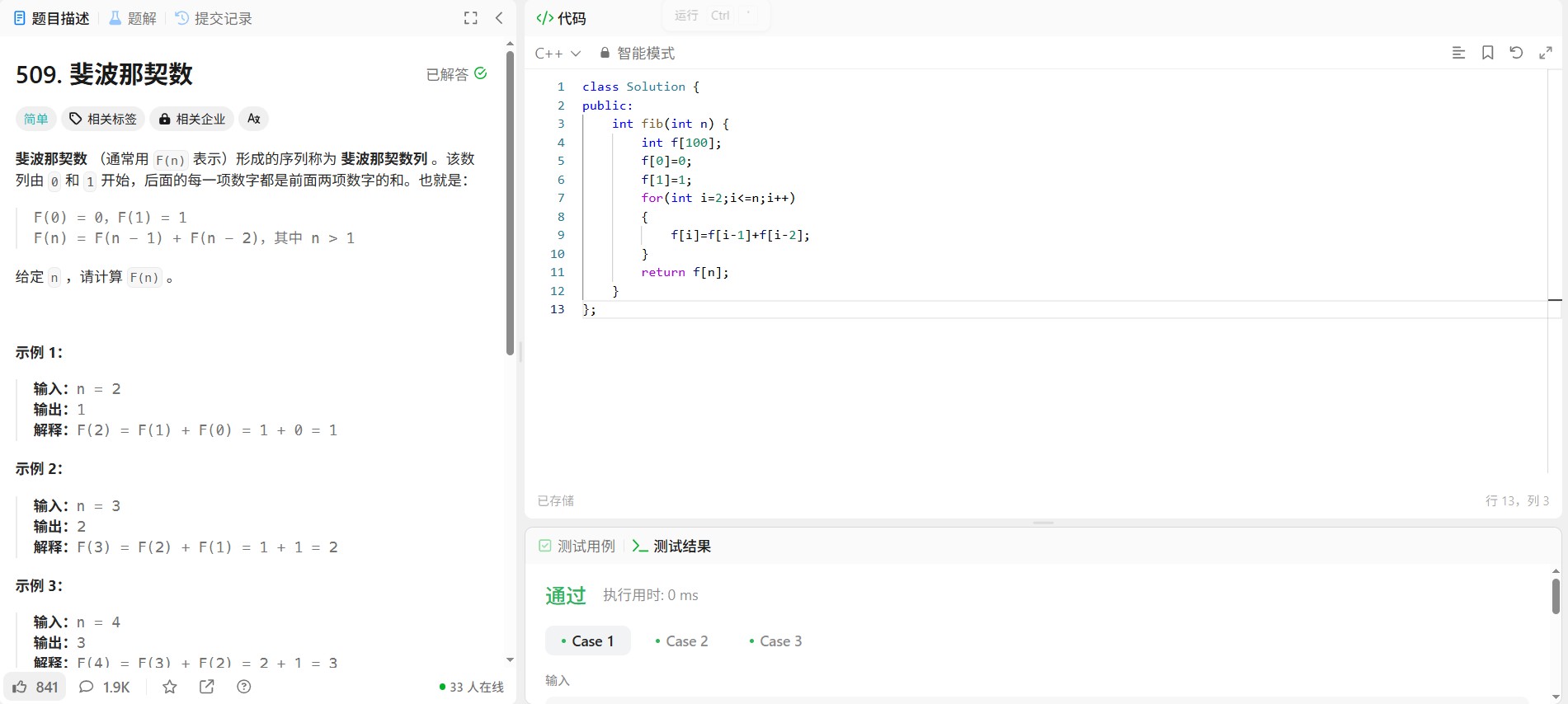
泰波那契数列是一个充满数学趣味的递推序列：从第3项开始，每个数均为前三个数的和（即Tₙ₊₃ = Tₙ + Tₙ₊₁ + Tₙ₊₂）。当给定整数n时，需要高效计算出第n项的值。面对此类递推问题，传统的递归方法可能因重复计算导致效率低下，因此动态规划成为破解的关键。

二：解题思路与过程

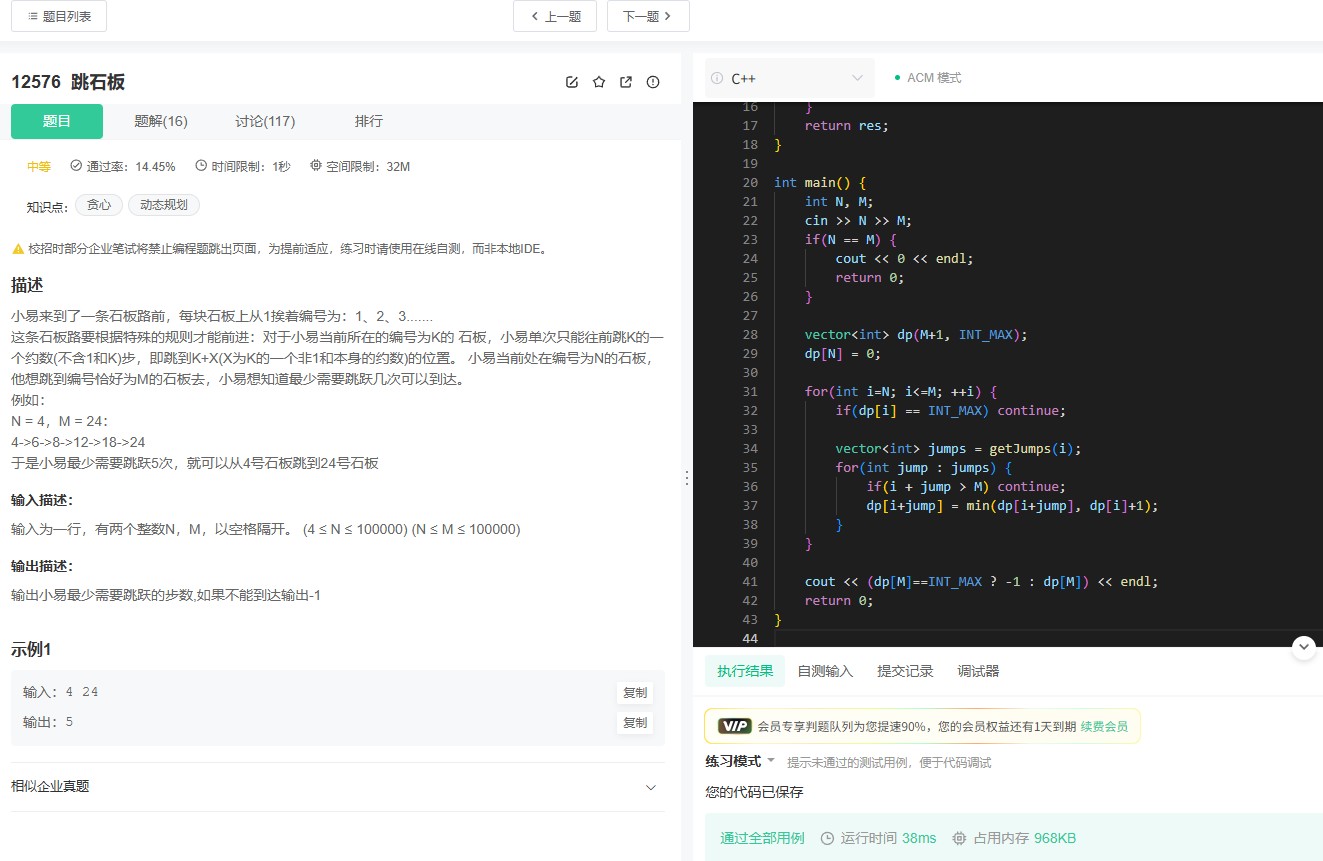
动态规划的核心在于“以空间换时间”：通过存储已计算出的中间结果，避免重复递归。代码中首先初始化数组dp，前3项分别赋值0、1、1（符合数列定义）。随后从第4项开始循环，每次通过dp[i] = dp[i-1] + dp[i-2] + dp[i-3]更新当前值，直至计算出第n项。此过程严格遵循递推公式，且因数组的有序访问，时间复杂度降至O(n)，远优于递归的指数级复杂度。

三：带注释的代码解析

class Solution {  
public:  
    int tribonacci(int n) {  
        // 创建固定长度数组（因题目n≤37，故无需动态分配）  
        int dp[38];  
        // 初始化前3项（边界条件）  
        dp[0] = 0;  
        dp[1] = 1;  
        dp[2] = 1;  
        // 从第3项开始递推计算  
        for (int i = 3; i <= n; i++) {  
            // 利用数组直接访问历史值，完成三步求和  
            dp[i] = dp[i-1] + dp[i-2] + dp[i-3];  
        }  
        // 返回目标项的结果  
        return dp[n];  
    }  
};