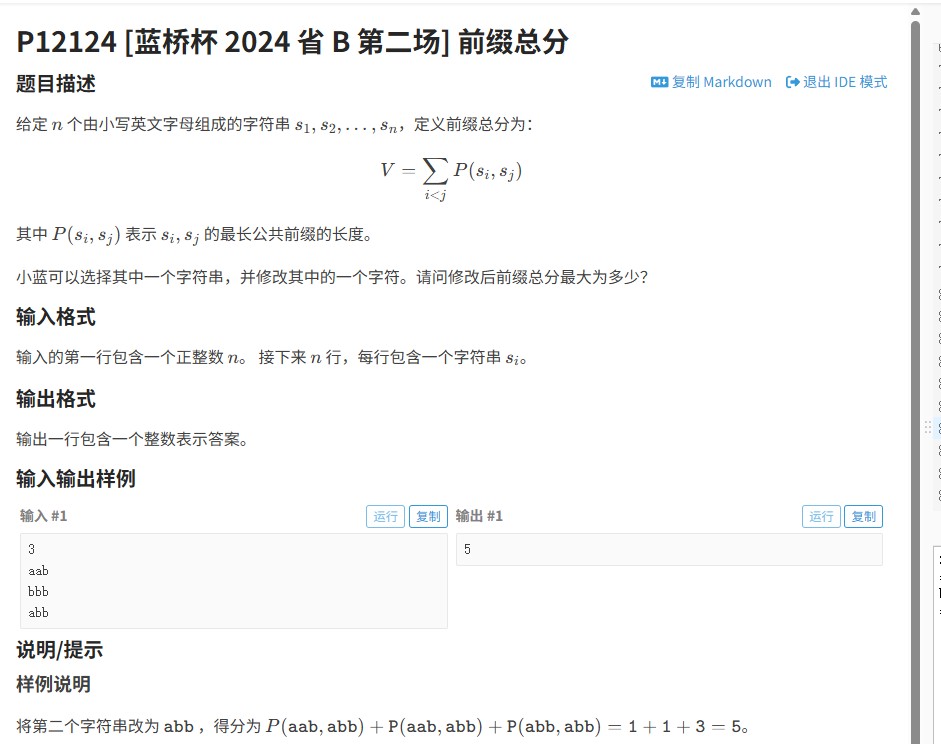
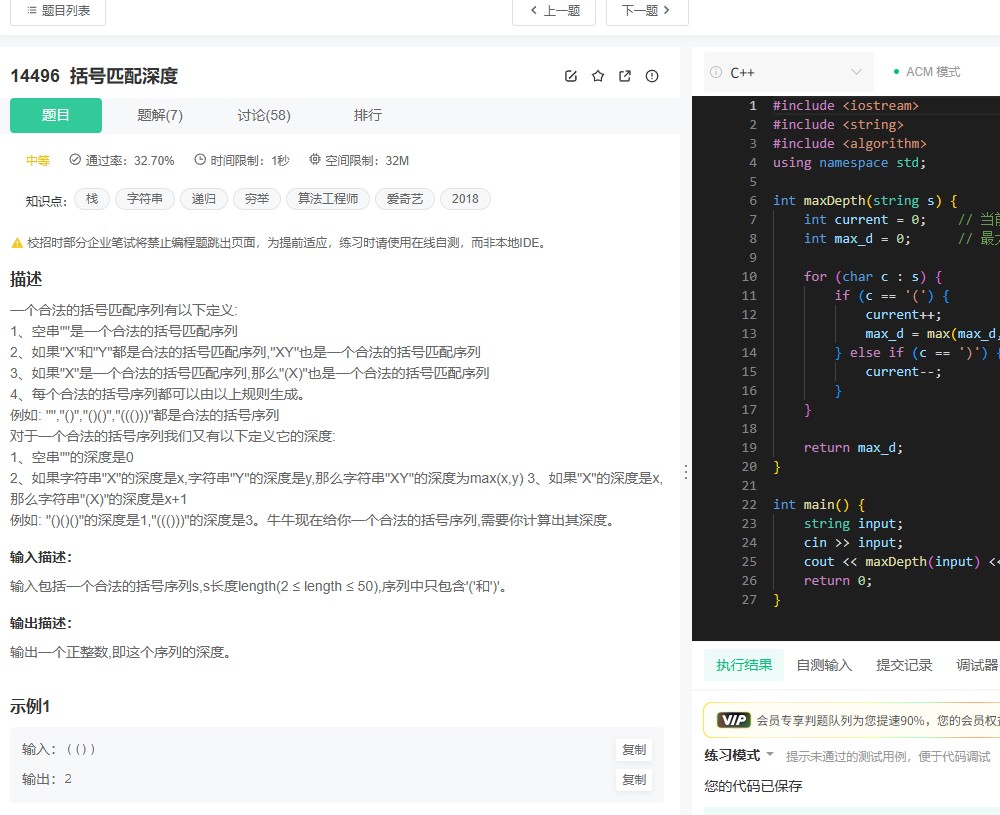
牛客4432题解题全解析：矩阵快速幂优化楼梯攀登问题（附C++代码）

一、题目解读

牛客4432题要求计算在n阶楼梯中，每次可爬1阶或2阶，共有多少种不同的攀登方式。该问题属于经典的动态规划类题目，需通过数学递推或矩阵乘法优化算法以应对较大数据规模。题目核心在于寻找高效计算路径总数的策略，并处理可能的数值溢出问题。

二、解题思路

解题采用矩阵快速幂算法。首先，构建初始状态矩阵{{1,1}, {1,0}}，表示第n阶路径数由前两阶递推。通过矩阵乘法实现状态转移，利用快速幂（二进制拆分）减少计算次数，最终通过模运算防止结果溢出。此思路将时间复杂度优化至O(log n)，避免递归或循环的O(n)耗时。

三、解题步骤

1. 边界处理：n≤0时返回0，n=1或2时直接返回对应路径数（1或2）。

2. 初始化矩阵：构建基础矩阵mat，其中mat[0][0]和mat[0][1]分别表示第n-1阶和第n阶的路径数。

3. 快速幂计算：调用matrixPower函数，通过二分递推计算mat^(n-2)，避免重复计算。

4. 结果组合：根据矩阵结果计算2*res[0][0] + res[1][0]并取模，得到最终路径数。

四、代码及注释

class GoUpstairs {  
public:  
    int countWays(int n) {  
        if(n <= 0) return 0;  // 边界条件：n非正时路径数为0  
        if(n == 1) return 1;  
        if(n == 2) return 2;  
        
        vector<vector<long>> mat = {{1,1}, {1,0}};  // 初始化状态矩阵（递推基础）  
        vector<vector<long>> res = matrixPower(mat, n-2);  // 计算矩阵的n-2次幂  
        return (2*res[0][0] + res[1][0]) % 1000000007;  // 组合结果并取模防溢出  
    }  
   
    vector<vector<long>> matrixMultiply(vector<vector<long>>& a, vector<vector<long>>& b) {
        vector<vector<long>> res(2, vector<long>(2));
        res[0][0] = (a[0][0]*b[0][0] + a[0][1]*b[1][0]) % 1000000007;
        res[0][1] = (a[0][0]*b[0][1] + a[0][1]*b[1][1]) % 1000000007;
        res[1][0] = (a[1][0]*b[0][0] + a[1][1]*b[1][0]) % 1000000007;
        res[1][1] = (a[1][0]*b[0][1] + a[1][1]*b[1][1]) % 1000000007;
        return res;
    }
    
    vector<vector<long>> matrixPower(vector<vector<long>>& mat, int p) {
        vector<vector<long>> res = {{1,0}, {0,1}};
        while(p > 0) {
            if(p & 1) res = matrixMultiply(res, mat);
            mat = matrixMultiply(mat, mat);
            p >>= 1;
        }
        return res;
    }
};

注释说明：

● matrixMultiply：实现矩阵乘法，通过分步计算每个元素并取模。

● matrixPower：采用快速幂算法，通过二进制拆分指数，减少乘法次数。

五、总结

本解法通过矩阵快速幂将楼梯攀登问题的复杂度从线性降至对数级，适用于大规模数据场景。核心在于将递推关系转化为矩阵乘法，并利用二进制拆分优化幂运算。此外，模运算保证了结果在限定范围内的正确性。该思路可扩展至其他需递推优化的动态规划问题，具有一定通用性。