力扣104题：二叉树的最大深度 - 递归解法详解与代码实现

内容简介

本文深入解析了力扣104题"二叉树的最大深度"的递归解法。通过简洁优雅的递归实现，展示了如何高效计算二叉树的深度。文章包含完整注释代码、算法思路讲解和复杂度分析，帮助读者理解递归在树结构问题中的应用。

算法思路

‌1.递归终止条件‌：当节点为空时返回深度0

‌2.递归计算‌：分别计算左右子树的深度

‌3.结果合并‌：取左右子树深度的最大值加1作为当前节点的深度

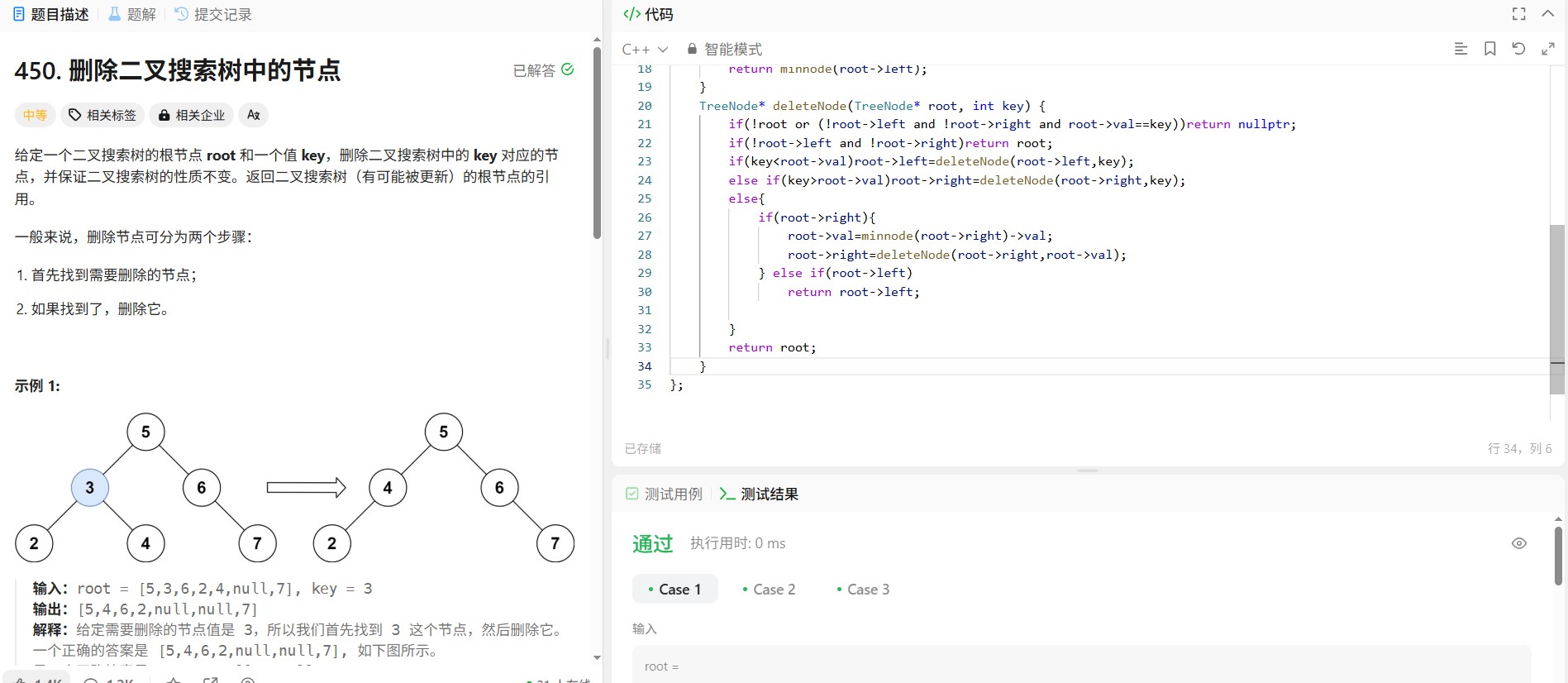
代码实现（带详细注释）

class Solution {
public:
    int maxDepth(TreeNode* root) {
        // 基本情况：空节点的深度为0
        if (!root) 
            return 0;
        
        // 递归计算左右子树的深度，取较大值加1
        // 当前节点的深度 = max(左子树深度, 右子树深度) + 1
        return max(maxDepth(root->left), maxDepth(root->right)) + 1;
    }
};

复杂度分析

‌时间复杂度‌：O(n)，需要访问树中的每个节点

‌空间复杂度‌：O(h)，递归栈空间取决于树的高度

优化方向

‌迭代解法‌：使用层序遍历(BFS)替代递归

‌尾递归优化‌：在某些编译器中可能优化递归调用

‌并行计算‌：对大规模树可考虑并行处理子树

总结

二叉树最大深度问题是递归算法的经典应用场景，通过分治思想将问题分解为子问题求解。理解这种解法有助于掌握树结构处理的基本模式和递归思维。