牛客4579题：钓鱼比赛——概率计算与比较

一、题目解读

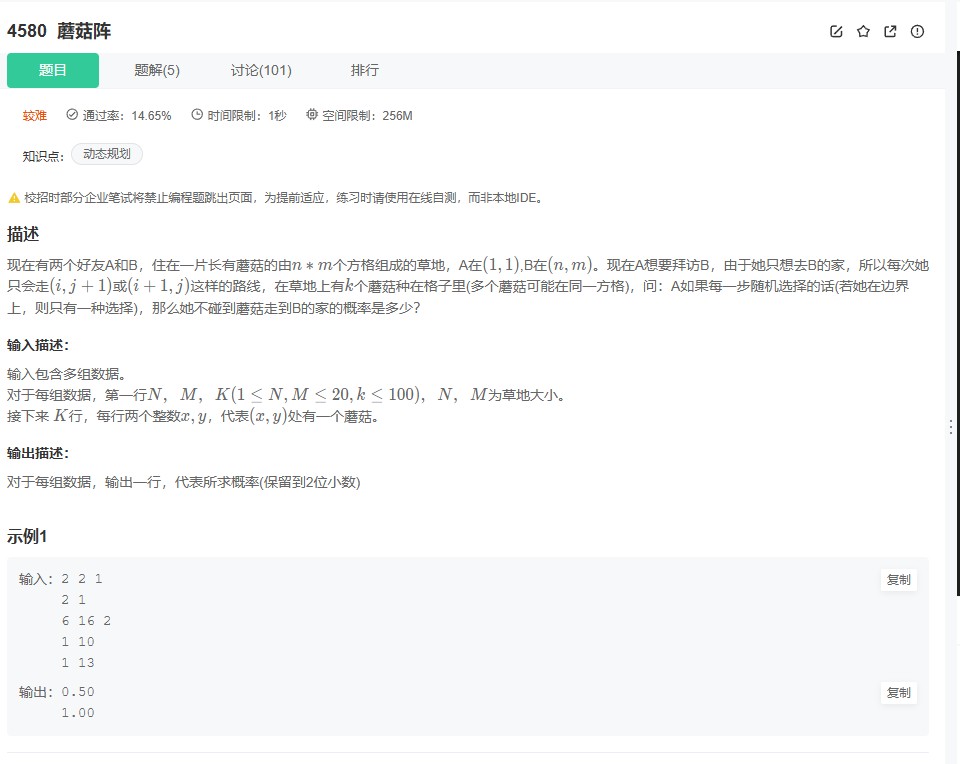
牛客4579题要求解决一个基于网格的概率计算问题：给定一个n×m的矩阵，每个元素表示对应位置钓到鱼的概率。用户需根据输入的坐标(x,y)和尝试次数t，比较该位置钓到鱼的累积概率与全区域平均概率的累积概率，并输出结果（"equal"、"cc"或"ss"）。题目强调坐标从1开始，需处理浮点数精度问题。

二、解题思路

1. 数据读取与预处理：接收n、m、x、y、t，构建二维概率矩阵并计算总和，避免重复计算。

2. 平均概率计算：总概率除以网格总数，得到全局平均概率。

3. 目标位置概率：利用公式 1 - (1 - p)^t 计算单点累积概率，减少浮点数误差。

4. 比较与输出：通过高精度比较（abs() < 1e-6）判断概率差异，输出对应结果及概率值。

三、解题步骤

1. 输入解析：依次读取n、m、x、y、t，初始化矩阵。

2. 矩阵构建与总概率统计：双层循环读取元素，同步累加 total。

3. 核心计算：

○ 计算平均概率 avg_p = total / (n * m)。

○ 计算目标位置概率 cc_p = grid[x-1][y-1]（需转换坐标）。

○ 分别计算累积概率 cc_prob 和 ss_prob 并比较。

4. 输出优化：使用 fixed << setprecision(2) 确保概率输出格式固定小数点2位。

四、代码与注释

#include <iostream>
#include <vector>
#include <cmath>
#include <iomanip>
using namespace std;

void solve() {
    int n, m, x, y, t;
    while (cin >> n >> m >> x >> y >> t) {
        vector<vector<double>> grid(n, vector<double>(m));
        double total = 0.0;
        
        // 读取概率矩阵并计算总和
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < m; ++j) {
                cin >> grid[i][j];
                total += grid[i][j];
            }
        }
        
        // 计算平均概率
        double avg_p = total / (n * m);
        double cc_p = grid[x-1][y-1]; // 题目中坐标从1开始
        
        // 计算至少钓到一条鱼的概率
        double cc_prob = 1 - pow(1 - cc_p, t);
        double ss_prob = 1 - pow(1 - avg_p, t);
        
        // 比较概率并输出结果
        cout << fixed << setprecision(2);
        if (abs(cc_prob - ss_prob) < 1e-6) {
            cout << "equal" << endl << cc_prob << endl;
        } else if (cc_prob > ss_prob) {
            cout << "cc" << endl << cc_prob << endl;
        } else {
            cout << "ss" << endl << ss_prob << endl;
        }
    }
}

int main() {
    solve();
    return 0;
}

五、总结

该解法通过精准的累积概率公式与高精度比较，高效解决了网格概率对比问题。关键点在于：

1. 坐标转换适配题目要求；

2. 避免多次计算总和提升效率；

3. 利用 pow() 简化累积概率计算；

4. 浮点数比较采用安全阈值。

可进一步优化输入流的效率或概率计算的数学简化。