洛谷P3365题解：二叉树与最长递增子序列的巧妙结合解决改造二叉树

一、题目解读

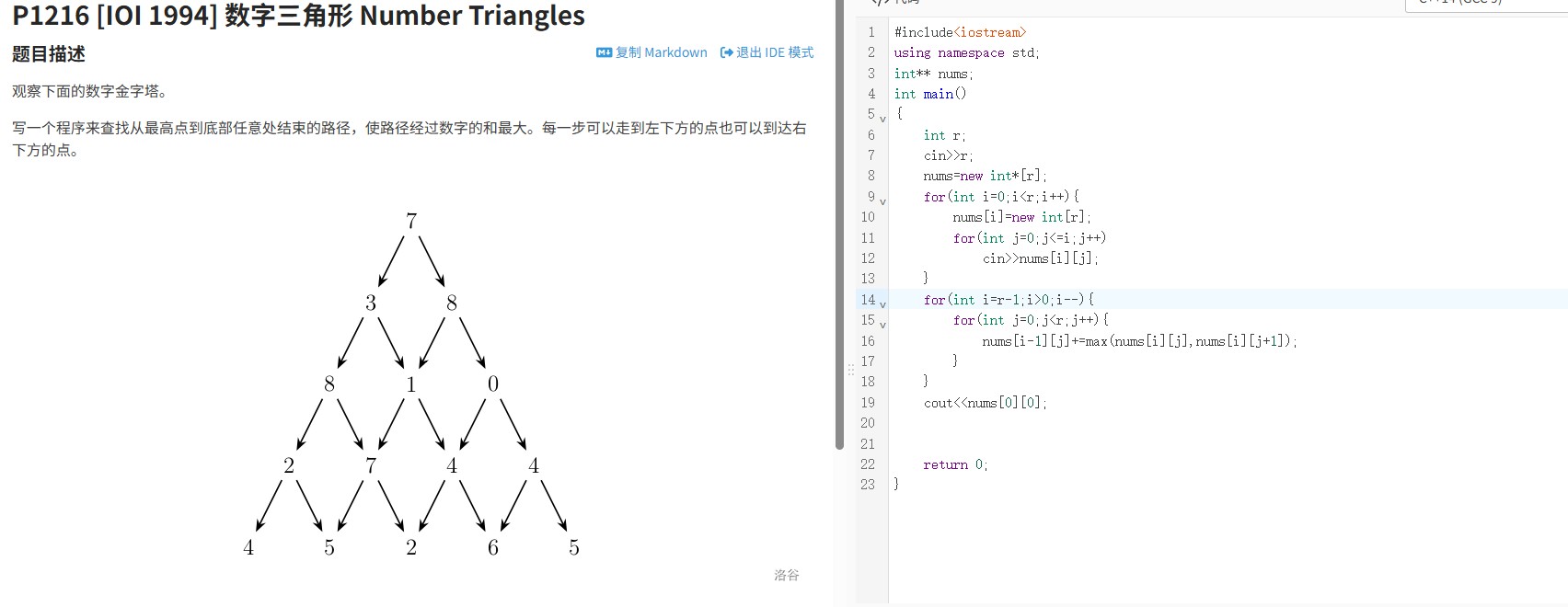
洛谷P3365题目要求给定一棵二叉树的中序遍历结果及部分边信息，求解其节点值的最长非递增子序列长度。本质是将树结构转化为序列问题，通过动态规划求解关键路径。

二、解题思路

核心思想为：

1. 构建二叉树：利用边信息（父节点与左右子节点关系）递归生成树结构；

2. 中序遍历：获取节点值序列，因中序遍历保证左子树→根→右子树的顺序；

3. LIS算法：通过动态规划计算序列的最长递增子序列（LIS）长度，其补集即为非递增子序列长度。

三、解题步骤

1. 输入处理：读取节点值数组vals及边信息edges；

2. 构建二叉树：通过buildTree函数，利用边关系连接节点；

3. 中序遍历：调用inorder递归函数，将节点值存入seq序列；

4. 计算LIS：使用lengthOfLIS函数，通过二分查找优化动态规划，返回LIS长度；

5. 输出结果：总节点数减去LIS长度即为答案。

四、代码与注释

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

// 构建二叉树
TreeNode* buildTree(int n, const vector<int>& vals, const vector<pair<int, int>>& edges) {
    vector<TreeNode*> nodes(n + 1);
    for (int i = 1; i <= n; ++i) {
        nodes[i] = new TreeNode(vals[i - 1]);
    }
    
    for (int i = 2; i <= n; ++i) {
        int fa = edges[i - 2].first;
        int ch = edges[i - 2].second;
        if (ch == 0) {
            nodes[fa]->left = nodes[i];
        } else {
            nodes[fa]->right = nodes[i];
        }
    }
    return nodes[1];
}

// 中序遍历收集节点值
void inorder(TreeNode* root, vector<int>& seq) {
    if (!root) return;
    inorder(root->left, seq);
    seq.push_back(root->val);
    inorder(root->right, seq);
}

// 计算最长递增子序列长度
int lengthOfLIS(vector<int>& nums) {
    vector<int> dp;
    for (int num : nums) {
        auto it = lower_bound(dp.begin(), dp.end(), num);
        if (it == dp.end()) {
            dp.push_back(num);
        } else {
            *it = num;
        }
    }
    return dp.size();
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    
    int n;
    cin >> n;
    
    vector<int> vals(n);
    for (int i = 0; i < n; ++i) {
        cin >> vals[i];
    }
    
    vector<pair<int, int>> edges(n - 1);
    for (int i = 0; i < n - 1; ++i) {
        cin >> edges[i].first >> edges[i].second;
    }
    
    TreeNode* root = buildTree(n, vals, edges);
    vector<int> seq;
    inorder(root, seq);
    
    int lis_len = lengthOfLIS(seq);
    cout << n - lis_len << endl;
    
    return 0;
}

五、总结

本解法关键在于中序遍历的特性与动态规划的结合。时间复杂度O(nlogn)，空间复杂度O(n)。掌握此类转化思路，可高效应对树与序列相关的算法问题。