力扣3619题岛屿计数问题：深度优先搜索与模K判断

一、题目解读

力扣3619题要求在一个由0和正整数构成的二维网格中，统计所有岛屿的数量。岛屿由相邻的正整数单元格组成（上下左右相邻），且岛屿内所有单元格的值之和必须能被整数k整除。题目需要返回满足条件的岛屿数量。这道题结合了经典的岛屿计数问题与数值求和的额外约束，需要设计高效的遍历与判断逻辑。

二、解题思路

采用深度优先搜索（DFS）策略，结合模K判断解决。核心思路如下：

1. 遍历网格每个单元格，若发现未访问的正整数单元格（陆地），启动DFS递归搜索。

2. 递归时累加当前岛屿的单元格值，并标记已访问。

3. 若岛屿总值sum对k取模为0，则计数+1。

4. 通过方向数组控制递归方向（上下左右），确保遍历所有相邻陆地。

此思路将岛屿搜索与数值条件判断紧密结合，避免了重复计算，同时满足题目要求。

三、解题步骤

1. 初始化参数：定义方向数组（上、右、下、左），确保递归遍历四个方向。

2. 外层遍历网格：使用双重循环检查每个单元格，若为陆地（>0）则执行DFS。

3. DFS递归搜索：

    边界检查：若越界或非陆地，终止递归。

    累加当前值并标记已访问。

    递归调用相邻方向，扩展岛屿范围。

4. 判断条件：若岛屿总值sum % k == 0，岛屿计数加1。

5. 最终返回总计数。

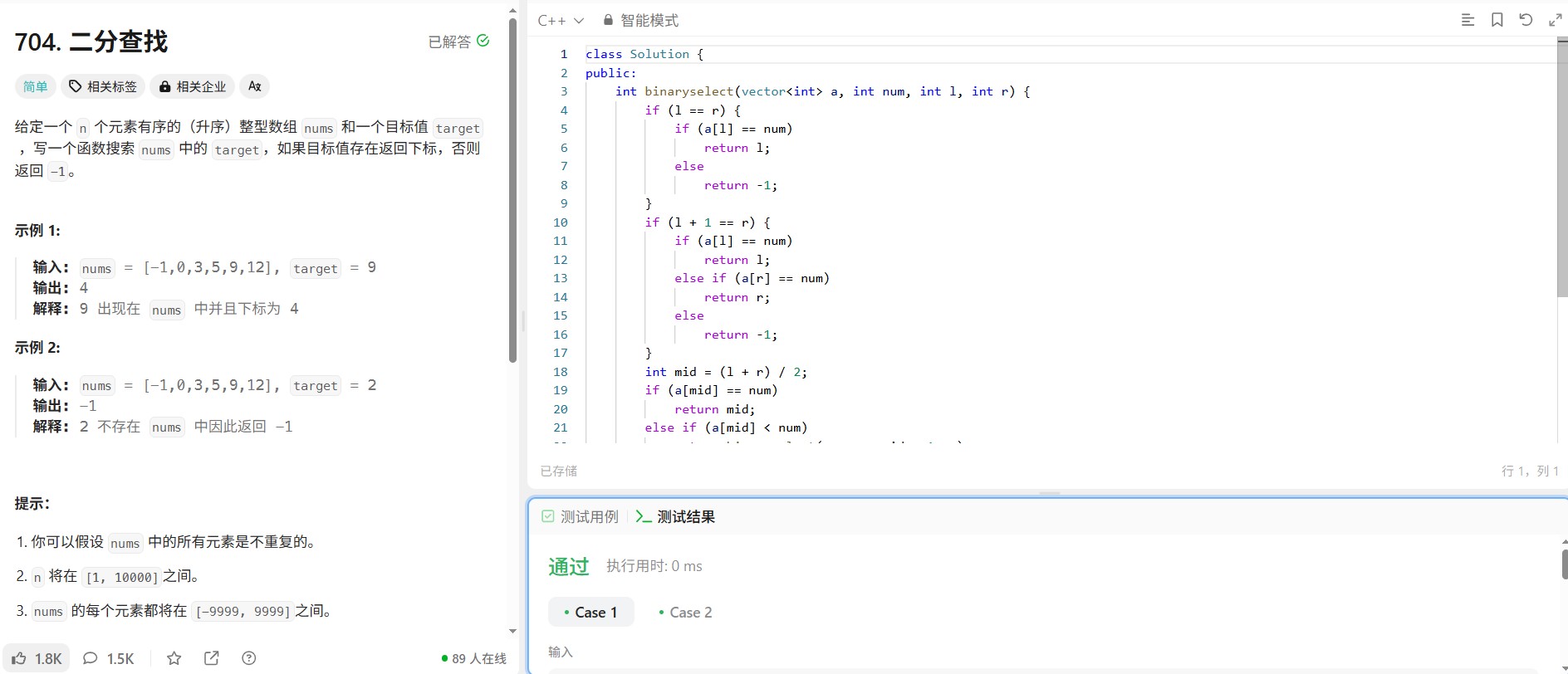
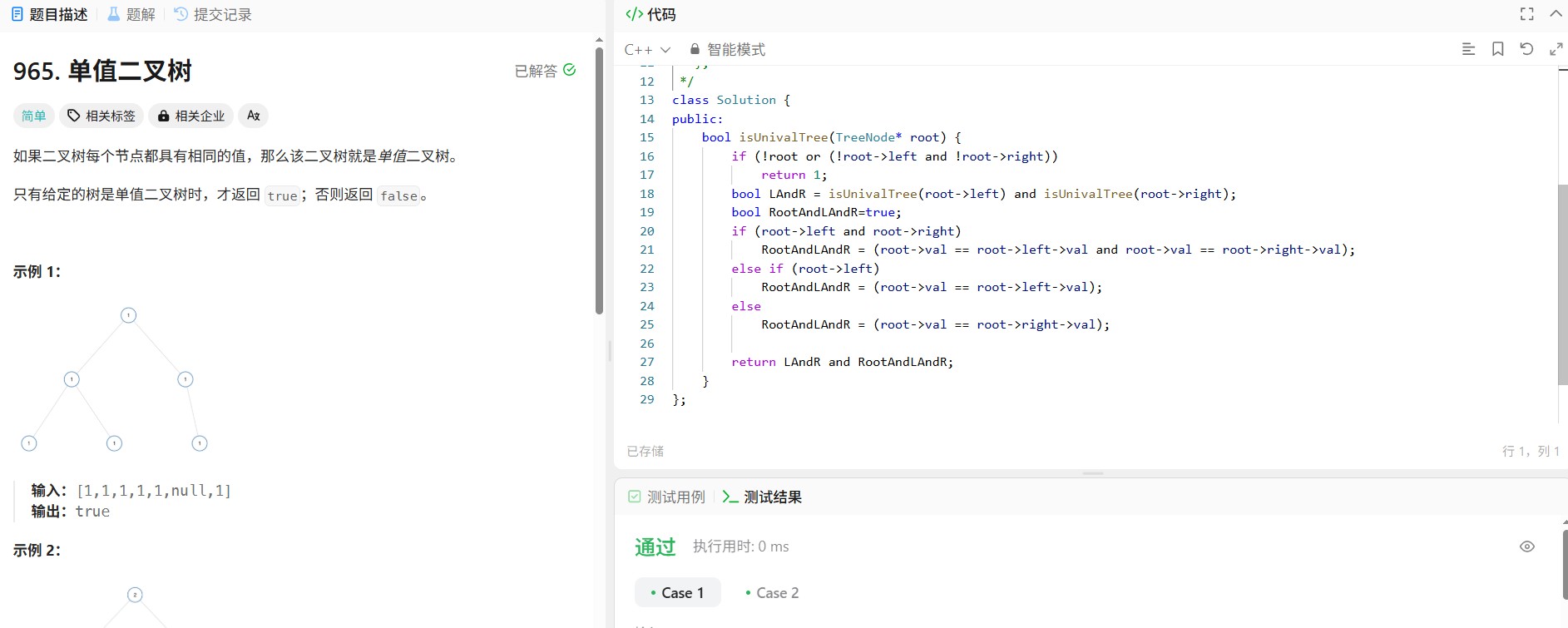
四、代码与注释

class Solution {
private:
    void dfs(vector<vector<int>>& grid, int i, int j, long long & sum, 
             const vector<pair<int, int>>& directions) {
        int m = grid.size(), n = grid[0].size();
        
        // 边界检查或当前单元格不是陆地
        if (i < 0 || i >= m || j < 0 || j >= n || grid[i][j] <= 0) {
            return;
        }
        
        // 累加当前单元格的值并标记为已访问
        sum += grid[i][j];
        grid[i][j] = -1;  // 标记为已访问
        
        // 向四个方向递归搜索
        for (const auto& dir : directions) {
            dfs(grid, i + dir.first, j + dir.second, sum, directions);
        }
    }
public:
    int countIslands(vector<vector<int>>& grid, int k) {
        if (grid.empty() || grid[0].empty()) return 0;
        int m = grid.size(), n = grid[0].size();
        int count = 0;
        
        // 定义方向数组：上、右、下、左
        vector<pair<int, int>> directions = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
        
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] > 0) {  // 发现新岛屿
                    long long sum = 0;
                    dfs(grid, i, j, sum, directions);
                    if (sum % k == 0) {
                        ++count;
                    }
                }
            }
        }
        return count;
    }
};

注释说明：代码通过DFS递归遍历岛屿，利用方向数组控制搜索路径，结合模K判断筛选符合条件的结果，实现高效解题。

五、总结

本文提供的解法利用深度优先搜索（DFS）递归遍历岛屿，并实时计算单元格总和，通过模K判断过滤符合条件的岛屿。该算法时间复杂度为O(MN)，空间复杂度为O(MN)（递归栈），适用于中等规模的网格数据。若需优化，可考虑BFS或并查集等其他算法路径。此外，代码结构清晰，注释详细，便于理解与复用。