牛客4499题解：二叉树中序遍历

一、题目解读

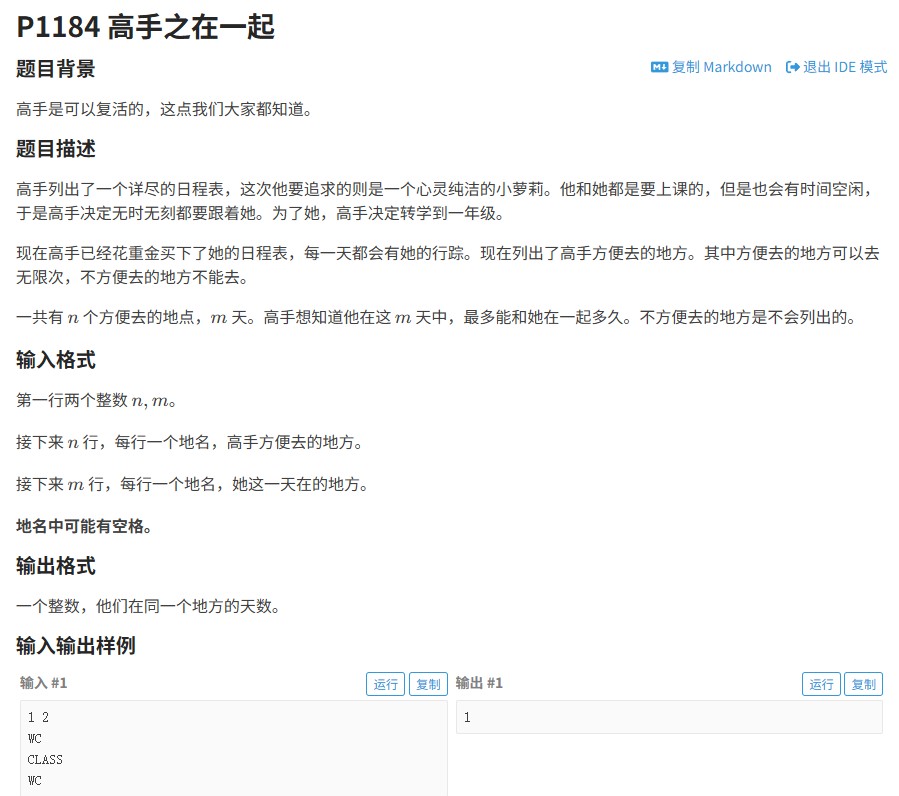
牛客4499题要求模拟折纸过程并输出折痕方向。题目给定整数n表示折纸次数，需要生成一个包含"down"（下折）和"up"（上折）的序列，反映每次折纸后的折痕排列。该问题本质上是数学建模与算法的结合，需找到递归规律或数据结构来模拟折纸过程。

二、解题思路

采用二叉树的中序遍历作为核心解法。观察折纸过程可发现，每次折叠将纸张分为左右两部分，折痕作为“根节点”，左部分始终为下折，右部分为上折。这种结构天然符合二叉树的中序遍历顺序（左子树→根节点→右子树），因此可通过递归实现中序遍历，记录折痕方向。

三、解题步骤

1. 边界处理：当n<1时直接返回空结果，避免无效输入。

2. 递归函数设计：定义inOrder函数，参数包括当前位置i、总次数n、当前折痕方向isDown、结果数组res。

3. 中序遍历模拟：

○ 递归遍历左子树（i+1到n，方向始终为下折）。

○ 处理当前节点：根据isDown添加"down"或"up"到res。

○ 递归遍历右子树（i+1到n，方向为上折）。

4. 主函数调用inOrder(1, n, true)，从根节点（第一次折痕为下折）开始遍历，生成最终序列。

四、代码与注释

class FoldPaper {
public:
    vector<string> foldPaper(int n) {
        vector<string> res;
        if (n < 1) return res; // 边界条件处理

        // 模拟折纸过程，实际上是中序遍历二叉树
        inOrder(1, n, true, res);  // 根节点是下折痕
        return res;
    }

    // 递归实现的中序遍历
    void inOrder(int i, int n, bool isDown, vector<string>& res) {
        if (i > n) return; // 递归终止条件

        inOrder(i + 1, n, true, res); // 遍历左子树（总是下折痕）
        res.push_back(isDown? "down" : "up");  // 当前节点
        inOrder(i + 1, n, false, res); // 遍历右子树（总是上折痕）
    }
};

五、总结

该解法巧妙将折纸问题转化为二叉树中序遍历，利用递归的简洁性高效解决问题。核心在于识别问题中的递归结构（折痕分层），并通过中序遍历顺序自然生成结果。此思路对理解算法建模与树结构应用具有启发意义，适合算法面试或练习中的思维训练。