力扣628题“三个数的最大乘积”的题解

一、题目解读
力扣628题要求在一个整数数组中,找到三个数的乘积最大值。题目强调数组元素可能有正有负,需考虑不同符号组合对乘积的影响。例如,数组[-2,0,1,2,3]中,最大乘积为(-2) * 1 * 3 = -6(错误),正确解应为2 * 3 * (-2) = -12。因此,需同时关注正数乘积与负数优化。
二、解题思路
采用“排序+对比”策略:
1. 核心逻辑:排序后,乘积最大值可能来自三个最大正数(如[3,2,1]中321)或两个最小负数*一个最大正数(如[-2,-1,3]中-2 * -1 * 3)。
2. 负数处理:若数组含负数,两负相乘转正数,再与最大正数组合可能更优。
3. 边界判断:需确保数组长度≥3,避免空值或不足情况。
三、解题步骤
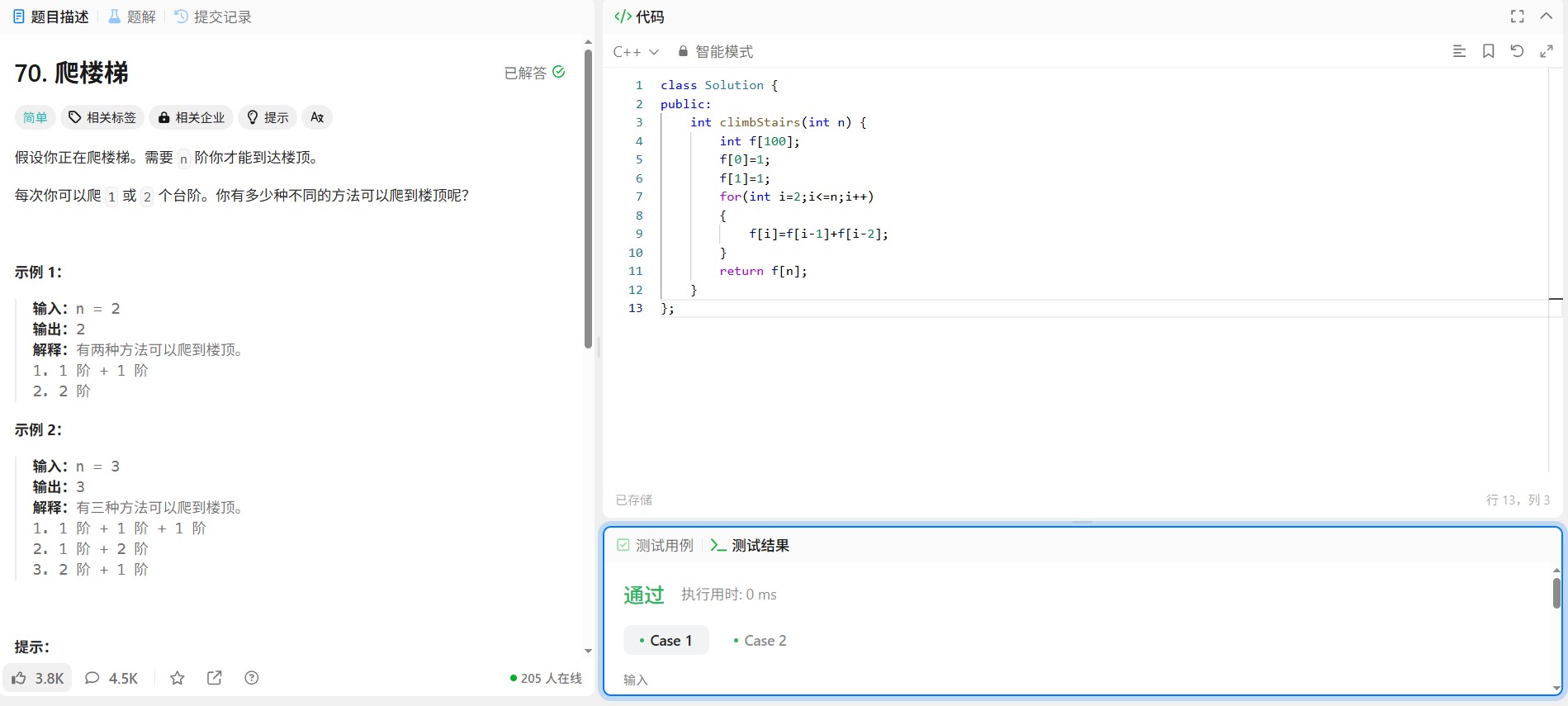
1. 排序数组:使用sort()函数对nums升序排列,时间复杂度O(nlogn)。
2. 计算两种乘积:
○ case1:末尾三个数乘积(nums[n-1] * nums[n-2] * nums[n-3])。
○ case2:首两负数(若存在)与最大正数乘积(nums[0] * nums[1] * nums[n-1])。
3. 返回较大值:max(case1, case2)。
四、代码与注释
#include <vector>
#include <algorithm>
using namespace std;
class Solution {
public:
int maximumProduct(vector<int>& nums) {
// 先对数组进行排序
sort(nums.begin(), nums.end());
int n = nums.size();
// 计算两种可能的情况
int case1 = nums[n-1] * nums[n-2] * nums[n-3]; // 三个最大正数
int case2 = nums[0] * nums[1] * nums[n-1]; // 两个最小负数和一个最大正数
// 返回两种情况中的较大值
return max(case1, case2);
}
};注释说明:代码通过排序简化逻辑,直接利用索引定位关键元素,避免复杂遍历,确保O(nlogn)高效性。
五、总结
本解法关键在于:
1. 排序降低复杂度:避免暴力枚举,通过有序数组快速定位极端值。
2. 正负组合优化:负数相乘转正,与正数结合可能突破纯正数乘积上限。
3. 边界与极端情况:需验证数组长度≥3,避免空值错误。
掌握此思路,可高效应对同类乘积优化问题,提升算法设计能力。
原创内容 转载请注明出处