当前位置：首页 > 提高组 > 2021年CSP-S廊桥分配问题解析（洛谷P7913）：基于贪心算法与优先级队列的解题思路

2021年CSP-S廊桥分配问题解析（洛谷P7913）：基于贪心算法与优先级队列的解题思路

9小时前

一、题目解读

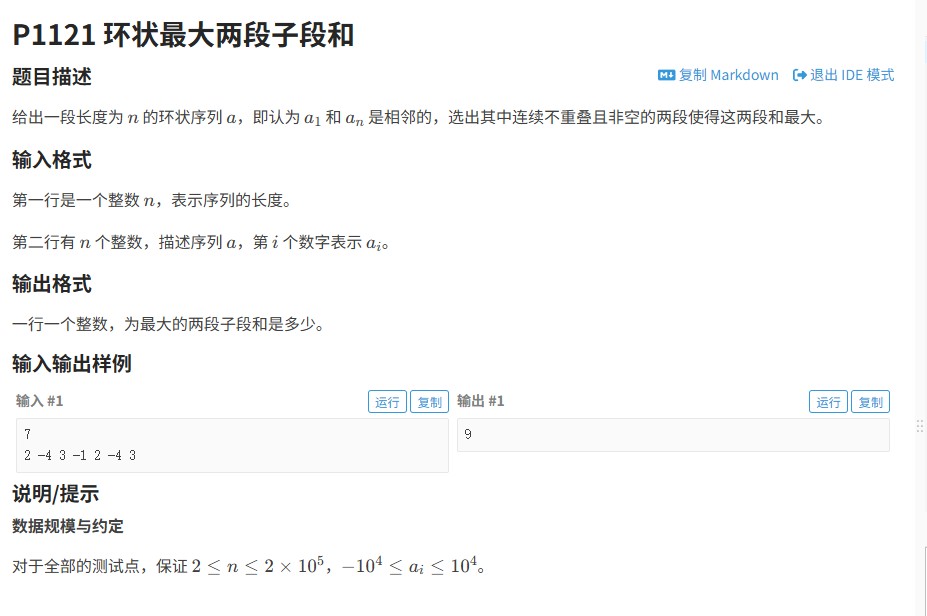
2021年CSP-S中的“廊桥分配”（洛谷P7913）是一个经典的资源分配问题。题目要求处理n个航班，每个航班有到达和离开时间，需在m1到m2个廊桥的限制下，计算使用不同数量的廊桥时能服务的最大航班数。核心在于高效分配廊桥资源，避免时间冲突，同时满足数量限制。

二、解题思路

采用贪心策略与优先级队列优化：

1. 航班排序：按到达时间升序排列，确保处理顺序符合时间逻辑。

2. 动态分配：使用两个优先队列——available存储当前可用廊桥的释放时间，in_use存储正在使用的廊桥及释放时间。

3. 分配逻辑：

优先使用已释放的廊桥（时间不冲突时）；

若无可用廊桥且剩余廊桥数未满，新建分配。

4. 前缀和优化：计算各廊桥数量的前缀和，便于快速查询不同k值下的最大服务数。

三、解题步骤

1. 输入与预处理：读取航班数据，按到达时间排序。

2. 初始化队列：available为空，in_use记录当前分配状态。

3. 循环分配：

释放过期廊桥（到达时间前已完成的航班）；

若available不空，分配最小释放时间的廊桥；

否则若廊桥数未满，新建分配。

4. 前缀和计算：累加各廊桥服务数，生成最终结果。

四、代码与注释

#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
using namespace std;

// 计算使用k个廊桥时能服务的最大航班数
vector<int> calculate_max_flights(const vector<pair<int, int>>& flights, int max_bridges) {
    vector<int> res(max_bridges + 1, 0);
    if (flights.empty()) return res;
    
    // 按到达时间排序航班
    vector<pair<int, int>> sorted_flights = flights;
    sort(sorted_flights.begin(), sorted_flights.end());
    
    // 优先队列存储可用廊桥的释放时间
    priority_queue<int, vector<int>, greater<int>> available;
    // 优先队列存储正在使用的廊桥的释放时间
    priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> in_use;
    
    int count = 0;
    for (const auto& flight : sorted_flights) {
        int arrive = flight.first;
        int depart = flight.second;
        
        // 释放已经完成的廊桥
        while (!in_use.empty() && in_use.top().first <= arrive) {
            available.push(in_use.top().second);
            in_use.pop();
        }
        
        // 如果有可用廊桥，则分配
        if (!available.empty()) {
            int bridge = available.top();
            available.pop();
            in_use.push({depart, bridge});
            count++;
            if (bridge <= max_bridges) {
                res[bridge]++;
            }
        }
        // 如果没有可用廊桥但还有未分配的廊桥，则分配新的
        else if (in_use.size() < max_bridges) {
            int bridge = in_use.size() + 1;
            in_use.push({depart, bridge});
            count++;
            if (bridge <= max_bridges) {
                res[bridge]++;
            }
        }
    }
    
    // 计算前缀和
    for (int i = 1; i <= max_bridges; ++i) {
        res[i] += res[i - 1];
    }
    
    return res;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    
    int n, m1, m2;
    cin >> n >> m1 >> m2;
    
    vector<pair<int, int>> domestic_flights(n);
    for (int i = 0; i < n; ++i) {
        cin >> domestic_flights[i].first >> domestic_flights[i].second;
    }
    vector<int> max_flights = calculate_max_flights(domestic_flights, m2);
    
    for (int i = m1; i <= m2; ++i) {
        cout << max_flights[i] << ';
    }
    cout << endl;
    
    return 0;
}