牛客3750题解题报告：滑动窗口最大值的高效解法（C++代码详解）

一、题目解读

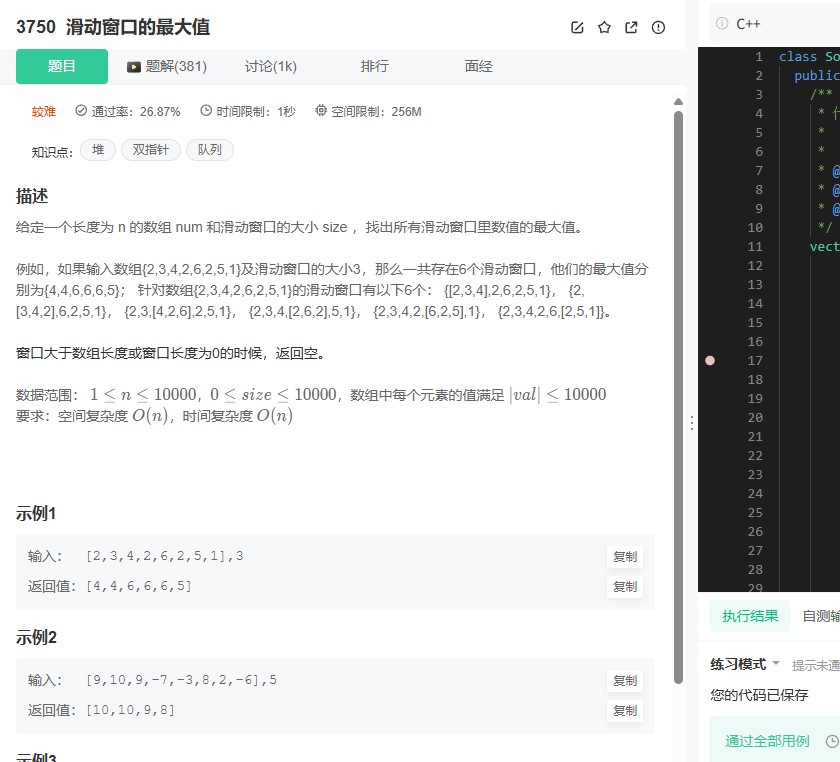
牛客3750题要求在一个给定的整数数组中，计算指定窗口大小下的滑动窗口最大值。例如，输入数组num=[1,3,-1,-3,5,3,6,7]，窗口大小为size=3时，需输出每个窗口内的最大值序列[3,5,5,6,7]。该题目考察对数组滑动窗口操作及高效数据结构的运用，核心在于如何在移动窗口时快速获取当前窗口的最大值。

二、解题思路

参考代码采用单调队列（Monotonic Queue）优化算法。通过维护一个存储元素下标的双端队列，确保队列中元素对应值始终单调递减。当新元素进入窗口时，通过弹出队尾较小值保持队列单调性，同时弹出队首过期元素（超出窗口范围），最终队首元素即为当前窗口最大值。该解法将时间复杂度降至O(n)，避免暴力遍历每个窗口。

三、解题步骤

1. 初始化：创建结果向量result和存储下标的单调队列dq。

2. 窗口遍历：

    判断队首下标是否超出窗口范围，若超出则弹出队首。

    从队尾弹出所有小于当前元素的值，维持队列单调递减。

    将当前下标加入队列。

3. 结果记录：当窗口形成（即当前索引≥窗口大小-1）时，将队首元素值加入结果向量。

4. 返回结果：最终返回最大值序列。

四、代码与注释

#include <vector>
#include <deque>
#include <stdexcept>
using namespace std;

class Solution {
public:
    vector<int> maxInWindows(vector<int>& num, int size) {
        vector<int> result;
        deque<int> dq; // 存储下标，保证队列中元素对应值单调递减

        for (int i = 0; i < num.size(); ++i) {
            // 移除超出窗口范围的元素
            while (!dq.empty() && dq.front() <= i - size) {
                dq.pop_front();
            }
            
            // 维护单调递减队列
            while (!dq.empty() && num[dq.back()] < num[i]) {
                dq.pop_back();
            }
            
            dq.push_back(i);
            
            // 当窗口形成后开始记录结果
            if (i >= size - 1) {
                result.push_back(num[dq.front()]);
            }
        }
        
        return result;
    }
};

注释说明：

● 使用deque存储下标而非元素值，避免值重复时的误判。

● 两个while循环分别处理过期元素和队列单调性，确保队首为窗口内最大值下标。

● 仅当窗口完整时记录结果，避免前缀无效计算。

五、总结

该解法巧妙利用单调队列的特性，将滑动窗口的遍历与动态维护最大值结合，实现线性时间复杂度。在实际应用中，此类算法适用于需要高效处理数据流或连续区间极值的问题，尤其在在线数据处理场景中表现优异。掌握单调队列思想对提升算法效率具有重要意义。