当前位置：首页 > 蓝桥杯 > 2016年蓝桥杯国赛B组机器人塔（洛谷P8644）解题全解析

2016年蓝桥杯国赛B组机器人塔（洛谷P8644）解题全解析

1天前

一、题目解读

2016年蓝桥杯国赛B组的“机器人塔”问题（洛谷P8644）是一个典型的组合数学与动态规划结合的题目。题目要求构建一个由A和B两种机器人组成的金字塔结构，其中每一层的机器人数量递减，且相邻机器人需满足特定规则。用户需根据给定的总机器人数量M和B机器人数量N，计算符合条件的金字塔方案总数。题目难点在于如何高效枚举所有合法状态，并验证其可行性。

二、解题思路

采用位运算与递推策略。首先，通过数学推导确定金字塔的总层数k（利用等差数列求和公式），若总机器人数无法构成完整金字塔则直接返回0。随后，利用二进制位掩码（bitmask）枚举底层所有可能的B机器人排列（用1表示B，0表示A），并通过逐层递推验证每一层的合法性：

每层机器人由下层相邻两个机器人合并生成：若下层相邻为相同类型，生成A；不同类型生成B。

若合并过程中剩余A/B数量不足，或层数验证不通过，则方案无效。

最终统计有效方案数。

三、解题步骤解析

1. 计算总层数k：利用k*(k+1)/2与总机器人数比较，确定唯一合法层数。

2. 底层排列枚举：使用二进制掩码遍历所有2^k种排列，统计B数量验证边界条件。

3. 逐层递推验证：

初始化当前层为底层掩码，剩余A/B数量。

对每一层，从高位到低位遍历，根据相邻位状态生成下一层，并更新剩余数量。

若某层合并失败或剩余数量耗尽，标记方案无效。

4. 统计有效方案：当所有层验证通过且剩余数量为0时，累加方案数。

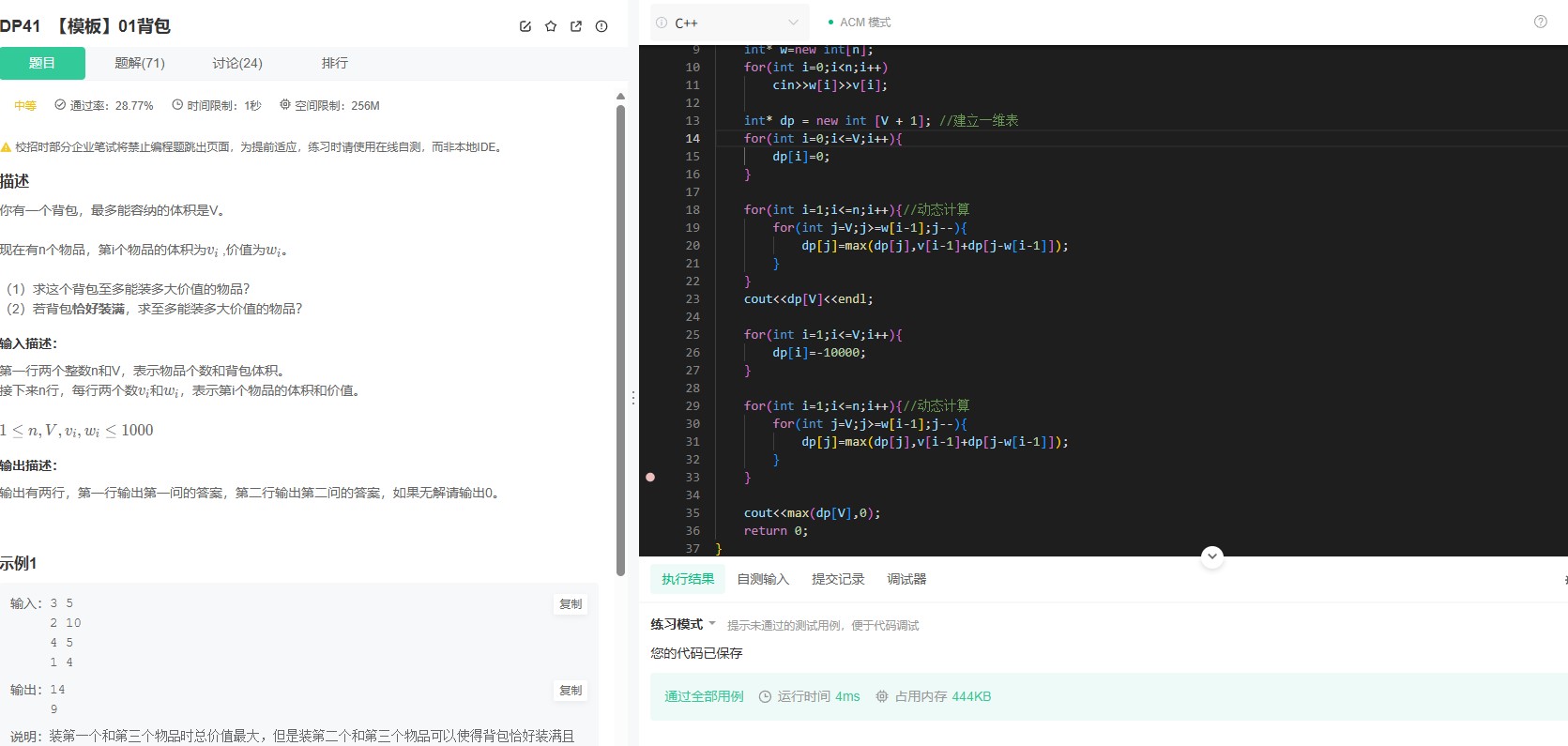
四、代码与注释

#include <iostream>
#include <vector>
using namespace std;

int count_bits(int x) { // 统计二进制中1的个数（即B数量）
    int cnt = 0;
    while (x) {
        cnt += x & 1;
        x >>= 1;
    }
    return cnt;
}

int main() {
    int M, N;
    cin >> M >> N;
    
    // 计算总层数k
    int total = M + N;
    int k = 1;
    while (k*(k+1)/2 < total) k++;
    
    if (k*(k+1)/2!= total) { // 层数不匹配直接退出
        cout << 0 << endl;
        return 0;
    }

    int ans = 0;
    // 枚举最底层所有可能的排列
    for (int mask = 0; mask < (1 << k); mask++) {
        int a = 0, b = count_bits(mask); // 统计当前层A/B数量
        if (b > N || (k - b) > M) continue; // 超出边界跳过
        
        int valid = 1;
        int current = mask; // 当前层掩码
        int remain_a = M - (k - b); // 剩余A需生成
        int remain_b = N - b; // 剩余B需生成
        
        for (int layer = k-1; layer >= 1 && valid; layer--) {
            int next_layer = 0; // 下一层掩码
            int new_a = 0, new_b = 0;
            
            for (int i = 0; i < layer; i++) {
                bool left = current & (1 << i); // 左机器人
                bool right = current & (1 << (i+1)); // 右机器人
                if (left == right) { // 生成A
                    if (remain_a <= 0) { valid = 0; break; }
                    remain_a--;
                    next_layer |= (0 << i); // 标记为A
                } else { // 生成B
                    if (remain_b <= 0) { valid = 0; break; }
                    remain_b--;
                    next_layer |= (1 << i); // 标记为B
                }
            }
            current = next_layer; // 进入下一层
        }
        
        if (valid && remain_a == 0 && remain_b == 0) { // 全部生成成功
            ans++;
        }
    }
    
    cout << ans << endl;
    return 0;
}